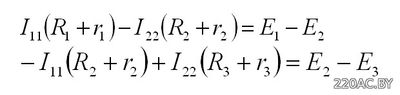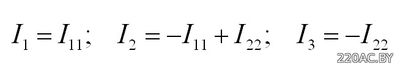Электрическая цепь – это соединение различных электрических или электронных деталей в одно. Для объединения используются проводники, которые пропускают через себя ток. Сами элементы могут самыми разнообразными – линейными, нелинейными, пассивными или активными. Любая электрическая цепь имеет в себе питание, включатель, провода, потребители тока. Она также должна быть замкнутой, иначе ток не сможет по ней протекать. Не являются электрической цепью заземляющие и зануляющие контуры.

Эта статья для тех, кто только начинает изучать теорию электрических цепей. Как всегда не будем лезть в дебри формул, но попытаемся объяснить основные понятия и суть вещей, важные для понимания. Итак, добро пожаловать в мир электрических цепей!

Электрические цепи

Электрическая цепь – это совокупность устройств, по которым течет электрический ток.

Рассмотрим самую простую электрическую цепь.  Из чего она состоит? В ней есть генератор – источник тока, приемник (например, лампочка или электродвигатель), а также система передачи (провода). Чтобы цепь стала именно цепью, а не набором проводов и батареек, ее элементы должны быть соединены между собой проводниками. Ток может течь только по замкнутой цепи. Дадим еще одно определение:

Электрическая цепь – это соединенные между собой источник тока, линии передачи и приемник.

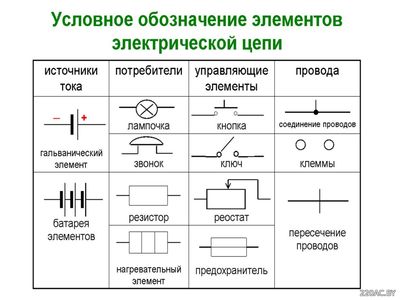
Конечно, источник, приемник и провода – самый простой вариант для элементарной электрической цепи. В реальности в разные цепи входит еще множество элементов и вспомогательного оборудования: резисторы, конденсаторы, рубильники, амперметры, вольтметры, выключатели, контактные соединения, трансформаторы и прочее.

Электрическая цепь

По какому фундаментальному признаку можно разделить все цепи электрического тока? По тому же, что и ток! Есть цепи постоянного тока, а есть – переменного. В цепи постоянного тока он не меняет своего направления, полярность источника постоянна. Переменный же ток периодически изменяется во времени как по направлению, так и по величине.

Сейчас переменный ток используется повсеместно.

Элементы электрических цепей

Все элементы электрических цепей можно разделить на активные и пассивные. Активные элементы цепи – это те элементы, которые индуцируют ЭДС. К ним относятся источники тока, аккумуляторы, электродвигатели. Пассивные элементы – соединительные провода и электроприемники.

Приемники и источники тока, с точки зрения топологии цепей, являются двухполюсными элементами (двухполюсниками). Для их работы необходимо два полюса, через которые они передают или принимают электрическую энергию. Устройства, по которым ток идет от источника к приемнику, являются четырехполюсниками. Чтобы передать энергию от одного двухполюсника к другому им необходимо минимум 4 контакта, соответственно для приема и передачи.

Резисторы – элементы электрической цепи, которые обладают сопротивлением. Вообще, все элементы реальных цепей, вплоть до самого маленького соединительного провода, имеют сопротивление. Однако в большинстве случаев этим можно пренебречь и при расчете считать элементы электрической цепи идеальными.

Существуют условные обозначения для изображения элементов цепи на схемах.

Нажмите на изображение чтобы увеличить

Вольт-амперная характеристика – фундаментальная характеристика элементов цепи. Это зависимость напряжения на зажимах элемента от тока, который проходит через него. Если вольт-амперная характеристика представляет собой прямую линию, то говорят, что элемент линейный. Цепь, состоящая из линейных элементов – линейная электрическая цепь. Нелинейная электрическая цепь – такая цепь, сопротивление участков которой зависит от значений и направления токов.

Какие есть способы соединения элементов электрической цепи? Какой бы сложной ни была схема, элементы в ней соединены либо последовательно, либо параллельно.

Нажмите на изображение чтобы увеличить

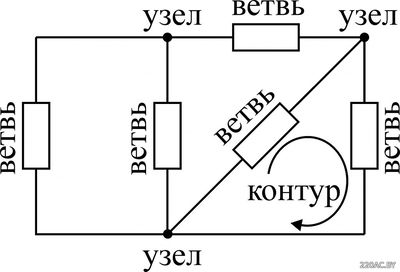
При решении задач и анализе схем используют следующие понятия:

• Ветвь – такой участок цепи, вдоль которого течет один и тот же ток;
• Узел – соединение ветвей цепи;
• Контур – последовательность ветвей, которая образует замкнутый путь. При этом один из узлов является как началом, так и концом пути, а другие узлы встречаются в контуре только один раз.

Чтобы понять, что есть что, взглянем на рисунок:

Нажмите на изображение чтобы увеличить

Классификация электрических цепей

По назначению электрические цепи бывают:

• Силовые электрические цепи;
• Электрические цепи управления;
• Электрические цепи измерения;

Силовые цепи предназначены для передачи и распределения электрической энергии. Именно силовые цепи ведут ток к потребителю.

Также цепи разделяют по силе тока в них. Например, если ток в цепи превышает 5 ампер, то цепь силовая. Когда вы щелкаете чайник, включенный в розетку, Вы замыкаете силовую электрическую цепь.

Электрические цепи управления не являются силовыми и предназначены для приведения в действие или изменения параметров работы электрических устройств и оборудования. Пример цепи управления – аппаратура контроля, управления и сигнализации.

Электрические цепи измерения предназначены для фиксации изменений параметров работы электрического оборудования.

Расчет электрических цепей

Рассчитать цепь – значит найти все токи в ней. Существуют разные методы расчета электрических цепей: законы Кирхгофа, метод контурных токов, метод узловых потенциалов и другие. Рассмотрим применение метода контурных токов на примере конкретной цепи.

Нажмите на изображение чтобы увеличить

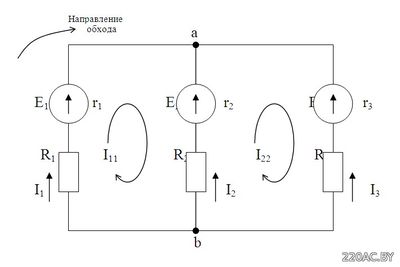
Сначала выделим контуры и обозначим ток в них. Направление тока можно выбирать произвольно. В нашем случае – по часовой стрелке. Затем для каждого контура составим уравнения по 2 закону Кирхгофа. Уравнения составляются так: Ток контура умножается на сопротивление контура, к полученному выражению добавляются произведения тока других контуров и общих сопротивлений этих контуров. Для нашей схемы:

Нажмите на изображение чтобы увеличить

Полученная система решается с подставкой исходных данных задачи. Токи в ветвях исходной цепи находим как алгебраическую сумму контурных токов

Нажмите на изображение чтобы увеличить

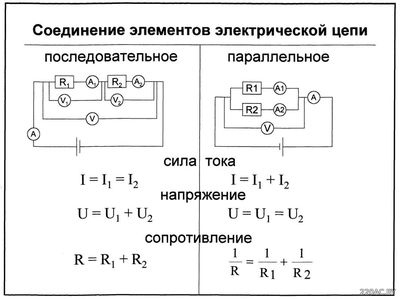
Последовательное соединение элементов цепи

В этом случае все элементы подключаются к цепи друг за другом. Последовательное соединение не дает возможности получить разветвленную цепь — она будет неразветвленной. На рис. 1 показан пример последовательного соединения элементов в цепи.

В нашем примере взяты два резистора. Резисторы 1 и 2 имеют сопротивления R1 и R2. Поскольку электрический заряд в этом случае не накапливается (постоянный ток), то при любом сечении проводника за определенный интервал времени проходит один и тот же заряд. Из этого вытекает, что сила тока в обоих резисторах равная:

I = I1 = I2

А вот напряжение на их концах суммируется:

U = U1 + U2

Согласно закону Ома, для всего участка цепи и для каждого резистора в отдельности полное сопротивление цепи будет:

R = R1 + R2

В случае последовательного соединения проводников напряжения и сопротивления можно выразить соотношением:

U1/U2 = R1/R2

Параллельное соединение проводников

Когда два проводника соединяются параллельно, электрическая цепь имеет два разветвления. Точки разветвления проводников называют узлами. В них электрический заряд не накапливается, т. е. электрический заряд, поступающий за определенный промежуток времени в узел, равен заряду, уходящему из узла за то же время. Из этого следует, что:

I = I1 + I2

где I — сила тока в неразветвленной цепи.

При параллельном соединении проводников напряжение на них будет одно и то же. Обозначим сопротивления параллельно соединенных двух проводников R1 и R2. Используя закон Ома для участков электрической цепи с данными сопротивлениями, можно выявить, что величина, обратная полному сопротивлению участка ab, равна сумме величин, обратных сопротивлениям отдельных проводников, т. е.:

1/R = 1/R1 + 1/R2

Из этого вытекает:

R = R1R2/(R1 + R2)

Данная формула справедлива только для определения общего сопротивления двух проводников, соединенных параллельно. Величину, обратную сопротивлению, называют проводимостью. При параллельном соединении проводников их сопротивления и сила тока связаны соотношением:

I1/I2 = R2/R1